Technical Report 310, c4e-Preprint Series, Cambridge

Authors: Jiaru Bai, Sebastian Mosbach, Connor J. Taylor, Dogancan Karan, Kok Foong Lee, Simon D. Rihm, Jethro Akroyd, Alexei A. Lapkin, and Markus Kraft*

Reference: Technical Report 310, c4e-Preprint Series, Cambridge, 2023

Associated Themes:
 

• Two self-driving laboratories are connected via a dynamic knowledge graph.
• The knowledge graph self-evolves to achieve research goals set by scientists.
• Collaborative closed-loop optimisation enables fast advances to the Pareto front.
• FAIR data provenance is captured for all data flow and experimental operations.
• The approach is scalable with seamless integration of additional laboratories.

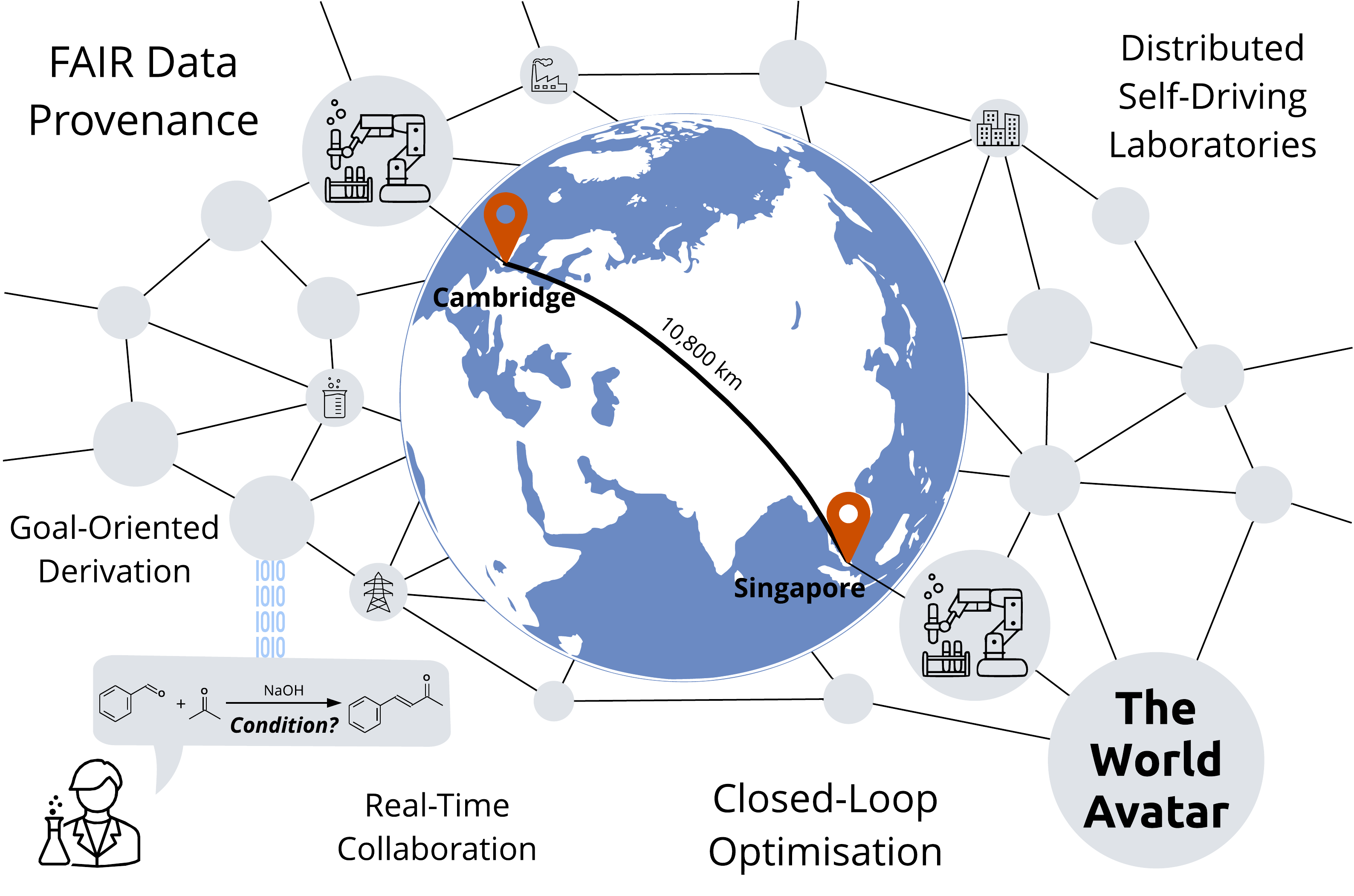The ability to integrate resources and share knowledge across organisations empowers scientists to expedite the scientific discovery process. This is especially crucial in addressing emerging global challenges that require global solutions. In this work, we develop an architecture to enable distributed self-driving laboratories as part of The World Avatar project, which seeks to demonstrate how to create an all-encompassing digital twin based on a dynamic knowledge graph. Our approach utilises ontologies to capture the data and material flows involved in design-make-test-analyse cycles, and employs autonomous agents as executable knowledge components to carry out the experimentation workflow. All data provenance is recorded following the FAIR principles, ensuring its accessibility and interoperability. We demonstrate the practical application of our framework by linking two robots in Cambridge and Singapore to achieve a collaborative closed-loop optimisation for a pharmaceutically-relevant aldol condensation reaction in real time. The knowledge graph evolves autonomously while progressing towards the research goals set by the scientist. The two robots effectively produced a Pareto front for the cost-yield optimisation problem over the course of three days of operation.

PDF (8.8 MB)