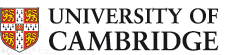A random cloud algorithm for the Schrödinger equation
- Numerical scheme for the one-dimensional time-dependent Schrödinger equation.
- Random Cloud Model in particle number formulation.
- Modification of the RCM to bounded domains.
- Analysis of the RCM processes for a particle in a potential well.
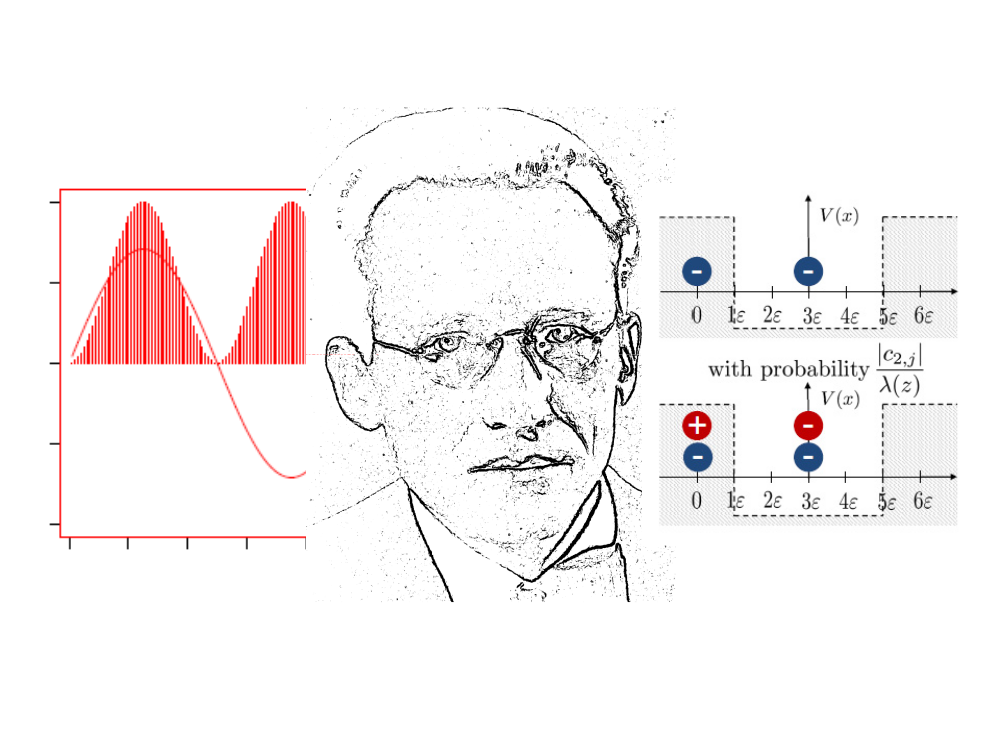In this paper we present a numerical scheme for the Random Cloud Model (RCM) on a bounded domain which approximates the solution of the time-dependent Schrödinger equation. The RCM is formulated as a Markov jump process on a particle number state space. Based on this process a stochastic algorithm is developed. It is shown that the algorithm reproduces the dynamics of the time-dependent Schrödinger equation for exact initial conditions on a bounded domain. The algorithm is then tested for two different cases. First, it is shown that the RCM reproduces the analytic solution for a particle in a potential well with infinite potential. Second, the RCM is used to study three cases with finite potential walls. It is found that the potential triggers processes, which produces RCM particles at a high rate that annihilate each other.
- This paper draws from preprint 173: A numerical scheme for the Random Cloud Model
- Access the article at the publisher: DOI: 10.1515/mcma-2017-0118
Associated Themes:
